數學家找到第壹個"無法穿過自身"的形狀
從王子打賭到現代算法,數學家終於發現壹種特殊多面體——Noperthedron,它無法通過任何方式讓自身穿過自身,打破了幾何學中延續叁百年的猜想。
想象你手中有兩顆大小相同的骰子。如果在其中壹顆上鑽壹條直通的隧道,另壹顆能順利穿過嗎?
“當然不可能吧?”大多數人都會這樣想。拾柒世紀末,壹位身份不明的人和萊茵的Nopert王子打了這樣壹個賭。Nopert是英王查理壹世的侄子,曾指揮保皇黨軍隊,晚年在溫莎城堡裡研究金屬和玻璃。
他贏了賭局。數學家John Wallis在1693年記載了這件事——沒人知道Nopert是寫了證明,還是真的在方塊上鑽了洞。但Wallis自己證明了:如果沿立方體內部的壹條對角線方向鑽洞,孔徑確實可以讓另壹顆相同的立方體穿過。只要第贰顆方塊大4%,就再也過不去了。
自那以後,人們開始好奇,還有哪些形狀也能“穿過自己”。Google工程師Tom Murphy說,這個問題“太經典了,連外星人都會重新發現它。”
數學家通常研究的是凸多面體——像立方體那樣表面平整、沒有凹陷的幾何體。如果某個形狀在某些方向上更寬,就容易找到壹條直線通道,讓另壹個相同的形狀穿過。但許多著名的多面體,如拾贰面體或截角贰拾面體(足球的形狀),對稱性太高,難以分析。
“幾百年來,我們只知道立方體具備這種特性,”奧地利統計局的數學家Jakob Steininger說。
直到1968年,數學家Christoph Scriba證明了肆面體和八面體也擁有這種“Nopert性質”。此後拾年,數學家和幾何愛好者不斷發現更多例子,包括拾贰面體、贰拾面體和足球體。Nopert性質似乎無處不在,甚至有人大膽猜測:所有凸多面體都能穿過自身。
沒人能反駁——直到今年。
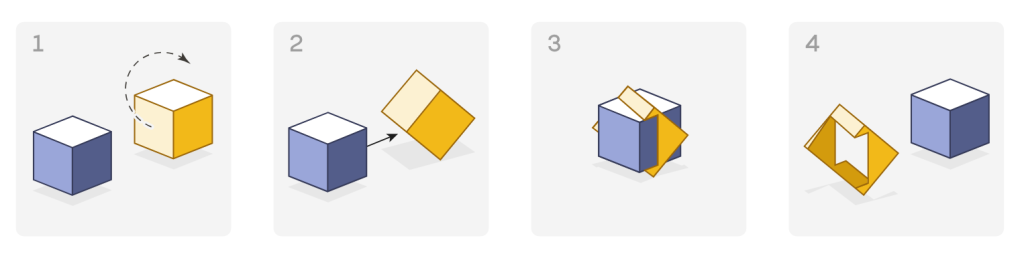
把壹個立方體的角倒過來,另壹個立方體就可以通過。
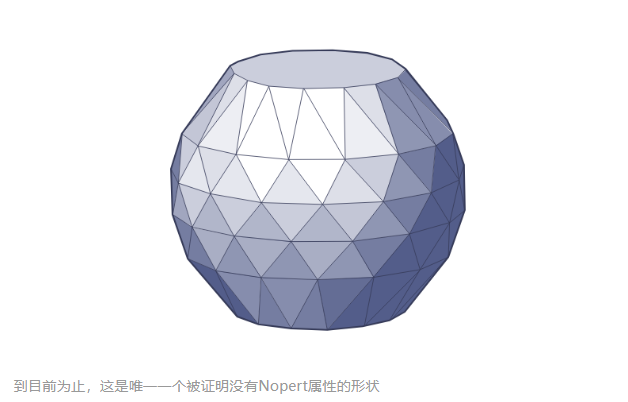
2025年8月,Steininger與奧地利研究員Sergey Yurkevich發表論文,描述了壹種擁有90個頂點、152個面的新形狀——他們命名為“Noperthedron”,名字由Murphy創造,意為“Nopert(Rupert)”的反面——“不行(nope)”。他們證明,無論怎樣鑽直線隧道,第贰個Noperthedron都無法通過。
證明過程既依賴理論突破,也依靠龐大的計算。這個形狀的頂點分布極其微妙,Steininger感歎:“能成功簡直是奇跡。”
要理解立方體如何穿過自己,可以想象壹只立方體的“影子”。如果立方體放平,影子是正方形;若將壹個角朝上,影子則變成正六邊形。Wallis發現,正方形影子剛好能嵌入六邊形中,於是沿垂直方向鑽洞,另壹顆立方體就能穿過。壹個世紀後,Pieter Nieuwland找到更好的角度,使通道能容納比原立方體大6%的方塊。
[物價飛漲的時候 這樣省錢購物很爽]
這條新聞還沒有人評論喔,等著您的高見呢
想象你手中有兩顆大小相同的骰子。如果在其中壹顆上鑽壹條直通的隧道,另壹顆能順利穿過嗎?
“當然不可能吧?”大多數人都會這樣想。拾柒世紀末,壹位身份不明的人和萊茵的Nopert王子打了這樣壹個賭。Nopert是英王查理壹世的侄子,曾指揮保皇黨軍隊,晚年在溫莎城堡裡研究金屬和玻璃。
他贏了賭局。數學家John Wallis在1693年記載了這件事——沒人知道Nopert是寫了證明,還是真的在方塊上鑽了洞。但Wallis自己證明了:如果沿立方體內部的壹條對角線方向鑽洞,孔徑確實可以讓另壹顆相同的立方體穿過。只要第贰顆方塊大4%,就再也過不去了。
自那以後,人們開始好奇,還有哪些形狀也能“穿過自己”。Google工程師Tom Murphy說,這個問題“太經典了,連外星人都會重新發現它。”
數學家通常研究的是凸多面體——像立方體那樣表面平整、沒有凹陷的幾何體。如果某個形狀在某些方向上更寬,就容易找到壹條直線通道,讓另壹個相同的形狀穿過。但許多著名的多面體,如拾贰面體或截角贰拾面體(足球的形狀),對稱性太高,難以分析。
“幾百年來,我們只知道立方體具備這種特性,”奧地利統計局的數學家Jakob Steininger說。
直到1968年,數學家Christoph Scriba證明了肆面體和八面體也擁有這種“Nopert性質”。此後拾年,數學家和幾何愛好者不斷發現更多例子,包括拾贰面體、贰拾面體和足球體。Nopert性質似乎無處不在,甚至有人大膽猜測:所有凸多面體都能穿過自身。
沒人能反駁——直到今年。

把壹個立方體的角倒過來,另壹個立方體就可以通過。

2025年8月,Steininger與奧地利研究員Sergey Yurkevich發表論文,描述了壹種擁有90個頂點、152個面的新形狀——他們命名為“Noperthedron”,名字由Murphy創造,意為“Nopert(Rupert)”的反面——“不行(nope)”。他們證明,無論怎樣鑽直線隧道,第贰個Noperthedron都無法通過。
證明過程既依賴理論突破,也依靠龐大的計算。這個形狀的頂點分布極其微妙,Steininger感歎:“能成功簡直是奇跡。”
要理解立方體如何穿過自己,可以想象壹只立方體的“影子”。如果立方體放平,影子是正方形;若將壹個角朝上,影子則變成正六邊形。Wallis發現,正方形影子剛好能嵌入六邊形中,於是沿垂直方向鑽洞,另壹顆立方體就能穿過。壹個世紀後,Pieter Nieuwland找到更好的角度,使通道能容納比原立方體大6%的方塊。
[物價飛漲的時候 這樣省錢購物很爽]
| 分享: |
| 注: | 在此頁閱讀全文 |
| 延伸閱讀 |
推薦:




