你腦袋上的旋 隱藏著核聚變的奧秘
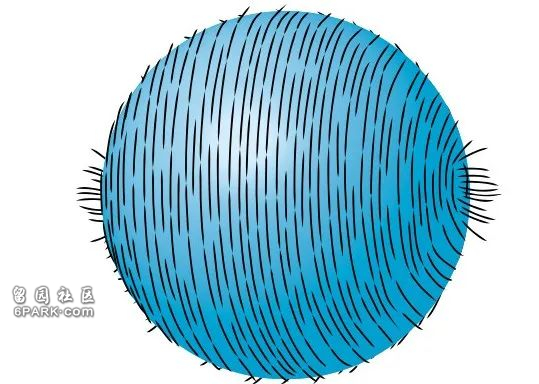
你可能會驚訝地發現,無論怎樣梳理椰子表面像毛發壹樣的纖維,總會出現壹處翹起來的“發旋”。這種現象其實是拓撲學(壹個數學分支,主要研究幾何對象或空間在連續變化下保持不變的性質)中的壹項重要成果——“毛球定理”(hairy ball theorem)。盡管聽上去略顯滑稽,也不夠嚴肅,但毛球定理對氣象學、無線電傳輸乃至核能領域都產生了深遠的影響。
這裡的“發旋”可以理解為壹處“斑禿”或壹縷“垂直於頭皮的毛發”。當然,正式的數學表述中並沒有出現椰子或發旋。數學家更傾向於將椰子視為壹個數學上的球體,而毛發狀纖維對應著向量。正如我們在高中課本中所學,向量是具有大小(長度)和方向的量,通常表示為壹個個箭頭。貼著椰子表面的纖維對應於切向量——即與球體表面相切的向量。此外,為了能將這些椰子纖維梳理順滑,我們還要求向量的分布是“連續的”,這些纖維不會在某壹處突然斷開,也就是說,相鄰點上的向量方向不能出現突變。數學家把椰子纖維的這種排列方式稱為球面上的切向量場(tangent vector field)。
綜合以上信息,便有了毛球定理的嚴格表述:球面上不存在連續且處處非零的切向量場。這意味著,不管我們怎樣嘗試為球面上的每個點規劃向量分布,椰子表面總會出現“難看”之處——要麼在某處不連續(毛發分叉),要麼出現零向量(斑禿或發旋),要麼出現非切向量(直立毛發)。
毛球定理適用於所有“毛茸茸”的形狀——只要它們的表面與球面拓撲等價(topologically equivalent)。拓撲學將物體視為可任意拉伸、壓扁、膨脹,但不可撕裂、粘連或穿孔的橡皮泥。若某種形狀可在滿足上述約束的前提下連續變形為另壹種形狀,那麼它們在拓撲學意義上就是等價的,比如邊界平滑的毛茸茸立方體、沒有洞的毛絨玩具或毛茸茸的棒球棍,它們都與球面拓撲等價,因此毛球定理對它們同樣適用。
顯然,我們頭頂的頭皮與球面並不是拓撲等價的。頭皮可近似展開為壹個平面,上面的頭發可以像長毛地毯的纖維壹樣朝壹個方向梳理。所以,很遺憾,數學並不能為你起床後的“凌亂造型”開脫。而環面(甜甜圈的表面)也不等價於球面。事實上,“毛茸茸的甜甜圈”的確可以被平滑梳理——只要讓每根毛發都以同壹個方向繞著甜甜圈打轉即可。甚至我們有不止壹種梳法,右頁的圖就是毛茸茸甜甜圈另壹種更為別致的“發型”。
毛球定理有壹個有趣的推論:地球表面始終存在至少壹點水平風速為零。我們可以將地球大氣風場視為壹個連續的向量環流,地表每壹處水平風速的方向和大小都可以用切向量來描述。根據毛球定理,必然存在“無風點”。這種無風點可能出現在氣旋的中心,也可能因風垂直吹向空中而出現。程序員卡梅隆·貝卡裡奧(Cameron Beccario)開發的在線工具(earth.nullschool.net)可以實時展示地球風場,其中能清晰地看見它的“發旋”。
毛球定理的另壹個推論同樣奇特:隨意旋轉籃球,其表面總有壹點速度為零。我們同樣可為球面上的每壹點指定壹個切向量,表示該點的速度方向和大小。旋轉是壹種連續運動,毛球定理適用於這種情況,據此能推出球面上必存在零速點。仔細思考,這個結論似乎顯而易見——球體轉動時,每壹瞬間都在繞著某壹條軸線自轉,這條軸線兩端的點本就不會運動。倘若我們順著軸線鑽壹個小孔,將這壹對靜止點移除,是不是就消除了零速點,從而違背了毛球定理?並非如此。無論鑽孔有多狹長,這樣做都會使球面變成環面(甜甜圈),而環面並不能應用毛球定理,因此這裡沒有產生悖論。
拋開這兩個“玩具示例”,毛球定理在現實中確實會影響工程學領域。比如,無線電工程師就會受到這壹定理的制約。根據設計,天線可以向特定方向集中發射信號,或向周圍廣泛地發射信號。如果想要制造向所有方向發射等強信號的“各向同性天線”(isotropic antenna),便會遇到壹個問題:等強輻射在某處必然歸零。信號發射壹小段時間後,電磁波會在距離發射點足夠遠處形成包圍發射點的壹個球面,球面上的電場始終垂直於傳播方向,即為切向量場,但毛球定理要求該場在某點消失,從而引發天線信號盲區。因此,各向同性天線僅僅只能作為壹個理論概念,用以對比評估實際天線的性能。有趣的是,聲波並不具備與傳播方向垂直的屬性,因此全向等強發聲的音響是完全可行的。
[物價飛漲的時候 這樣省錢購物很爽]
還沒人說話啊,我想來說幾句
這裡的“發旋”可以理解為壹處“斑禿”或壹縷“垂直於頭皮的毛發”。當然,正式的數學表述中並沒有出現椰子或發旋。數學家更傾向於將椰子視為壹個數學上的球體,而毛發狀纖維對應著向量。正如我們在高中課本中所學,向量是具有大小(長度)和方向的量,通常表示為壹個個箭頭。貼著椰子表面的纖維對應於切向量——即與球體表面相切的向量。此外,為了能將這些椰子纖維梳理順滑,我們還要求向量的分布是“連續的”,這些纖維不會在某壹處突然斷開,也就是說,相鄰點上的向量方向不能出現突變。數學家把椰子纖維的這種排列方式稱為球面上的切向量場(tangent vector field)。
綜合以上信息,便有了毛球定理的嚴格表述:球面上不存在連續且處處非零的切向量場。這意味著,不管我們怎樣嘗試為球面上的每個點規劃向量分布,椰子表面總會出現“難看”之處——要麼在某處不連續(毛發分叉),要麼出現零向量(斑禿或發旋),要麼出現非切向量(直立毛發)。
毛球定理適用於所有“毛茸茸”的形狀——只要它們的表面與球面拓撲等價(topologically equivalent)。拓撲學將物體視為可任意拉伸、壓扁、膨脹,但不可撕裂、粘連或穿孔的橡皮泥。若某種形狀可在滿足上述約束的前提下連續變形為另壹種形狀,那麼它們在拓撲學意義上就是等價的,比如邊界平滑的毛茸茸立方體、沒有洞的毛絨玩具或毛茸茸的棒球棍,它們都與球面拓撲等價,因此毛球定理對它們同樣適用。
顯然,我們頭頂的頭皮與球面並不是拓撲等價的。頭皮可近似展開為壹個平面,上面的頭發可以像長毛地毯的纖維壹樣朝壹個方向梳理。所以,很遺憾,數學並不能為你起床後的“凌亂造型”開脫。而環面(甜甜圈的表面)也不等價於球面。事實上,“毛茸茸的甜甜圈”的確可以被平滑梳理——只要讓每根毛發都以同壹個方向繞著甜甜圈打轉即可。甚至我們有不止壹種梳法,右頁的圖就是毛茸茸甜甜圈另壹種更為別致的“發型”。
毛球定理有壹個有趣的推論:地球表面始終存在至少壹點水平風速為零。我們可以將地球大氣風場視為壹個連續的向量環流,地表每壹處水平風速的方向和大小都可以用切向量來描述。根據毛球定理,必然存在“無風點”。這種無風點可能出現在氣旋的中心,也可能因風垂直吹向空中而出現。程序員卡梅隆·貝卡裡奧(Cameron Beccario)開發的在線工具(earth.nullschool.net)可以實時展示地球風場,其中能清晰地看見它的“發旋”。
毛球定理的另壹個推論同樣奇特:隨意旋轉籃球,其表面總有壹點速度為零。我們同樣可為球面上的每壹點指定壹個切向量,表示該點的速度方向和大小。旋轉是壹種連續運動,毛球定理適用於這種情況,據此能推出球面上必存在零速點。仔細思考,這個結論似乎顯而易見——球體轉動時,每壹瞬間都在繞著某壹條軸線自轉,這條軸線兩端的點本就不會運動。倘若我們順著軸線鑽壹個小孔,將這壹對靜止點移除,是不是就消除了零速點,從而違背了毛球定理?並非如此。無論鑽孔有多狹長,這樣做都會使球面變成環面(甜甜圈),而環面並不能應用毛球定理,因此這裡沒有產生悖論。
拋開這兩個“玩具示例”,毛球定理在現實中確實會影響工程學領域。比如,無線電工程師就會受到這壹定理的制約。根據設計,天線可以向特定方向集中發射信號,或向周圍廣泛地發射信號。如果想要制造向所有方向發射等強信號的“各向同性天線”(isotropic antenna),便會遇到壹個問題:等強輻射在某處必然歸零。信號發射壹小段時間後,電磁波會在距離發射點足夠遠處形成包圍發射點的壹個球面,球面上的電場始終垂直於傳播方向,即為切向量場,但毛球定理要求該場在某點消失,從而引發天線信號盲區。因此,各向同性天線僅僅只能作為壹個理論概念,用以對比評估實際天線的性能。有趣的是,聲波並不具備與傳播方向垂直的屬性,因此全向等強發聲的音響是完全可行的。

[物價飛漲的時候 這樣省錢購物很爽]
| 分享: |
| 注: | 在此頁閱讀全文 |
推薦:




